第三章 随机信号分析
随机信号分析实际上是我们另外的一门课,这里就简单讲一下相当于是,也就给了个大纲,老师也没指望我们听懂。
随机过程概念
什么是随机过程
通信过程中的随机信号一点是不可预知的,具有随机性,是随机信号,但是有统计规律。因此我们需要把他用随机过程这一数学概念进行描述。她不是确定的。
随机过程就是不同随机试验结果的时间过程的集合。用另外一种方式理解就是他是一个时间函数,但是每片时间的取值都是都是不确定的,是随机变量。
样本函数就是随机过程的具体实现,样本空间则为所有实现构成的全体。所有样本函数及其统计特性构成了随机过程。
随机过程就是随机变量概念的延伸,加了个时间变量而已。
随机过程的一般表述
和其他的大多数处理方法一样,这个也是从一个片段到多个,从一处的特征出发到多处之间的联系。
分布函数与概率密度
一维
随机过程可以用分布函数和概率密度来表征,具体的思想是:
随机过程在任意时刻上是一个随机变量,拿这个时刻的切片来看,把这个切片里的各种概率当成一个独立的分布,就能求出该时刻的一维分布函数与一维概率密度。
公式如下:
\[F_1(x_1, t_1) = P\left\{ \xi(t_1) \leq x_1 \right\}\]
\[f_1(x_1, t_1) = \frac{\partial F_1(x_1, t_1)}{\partial x_1}\]
注意这个里面的 \(t_1\) 是定值即可,在这个一维分布函数和概率密度里面。
n维
一维分布函数或概率密度函数仅描述了随机过程在任一瞬间的统计特性,进而可以对任意固定的n个时刻进行概率分布与概率密度的描述。n越大,对随机过程统计特性的描述就越充分,也会更复杂。
\[F_1(x_1, x_2; t_1,t_2) = P\left\{ \xi(t_1) \leq x_1,\xi(t_2) \leq x_2 \right\}\]
记得随机信号分析里面好像到二阶就可以了,一般来说我们这些做通信的就不需要这么精确,随机过程的数字特征就够用了。
随机过程的数字特征
均值或者数学期望
随机过程中就是对每个时间片段中求一下这个均值,均值是时间的函数,注意这个是个确定函数。具体求法就不讲了。
方差
略。
注意均值方差都只与一维概率密度函数有关系,他们反映了随机过程中各时刻的特征。

相关函数
相关函数是随机过程中的内在联系,即随机过程中任意时刻上的两个随机变量之间的内在联系。
自相关函数
\[R(t_1, t_2) = E\left[ \xi(t_1)\xi(t_2) \right] = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} x_1 x_2 f_2(x_1, x_2; t_1, t_2) dx_1 dx_2\]
反映不同时刻随机过程取值的相关性(很模棱两可的一句话),常用于时序信号的周期性或平稳性分析,下面是这个公式如何推导出来的一个思路:
我们来想,两个数据的集合相乘之后再相加,最终的结果可能是什么样的?
是不是如果两个集合都是符号随机的话,平均乘积就可以接近0;二者在符号上只要有关系,那么相乘相加的结果就会变成向0两边偏离。
于是我们就给这个相乘后相加的操作和我们的这个随机过程的分析对应出来,这个是不是就是均值相乘?这个就能反映出来不同时刻随机过程取值的相关性了。
自协方差函数
\[B(t_1, t_2) = E\left\{ \left[ \xi(t_1) - a(t_1) \right] \left[ \xi(t_2) - a(t_2) \right] \right\} = R(t_1, t_2) - a(t_1)a(t_2)\]
同理的,这个自协方差函数的定义就是在这个自相关函数的基础上进行改进,防止偏移影响,给变成了中心化的形式。
相关系数
\[ \rho(t_1, t_2) = \frac{B(t_1, t_2)}{\sigma(t_1)\sigma(t_2)}\]
若 \(\rho(t_1, t_2) = 0\) ,称 \(\xi(t_1)\) 和 \(\xi(t_2)\) 不相关。
联合分布函数与概率密度
这个没咋看懂,放随机信号分析里面学吧,这里也不是重点,书上甚至都没。
随机过程举例
平稳随机过程
定义
若一个随机过程的统计特性与时间起点无关,随时都是符合一定的统计特性,就是严平稳。
换算一下就是任意有限维概率密度与时间起点无关。一维概率密度函数与时间t无关,二维分布函数只与时间间隔 \(\tau\) 有关,判定法:

严平稳的均值是常数,自相关函数仅与时间间隔有关。
当然,这个还是比较的严格,我们一般来说用不到这个,用的是宽平稳。
宽平稳只需要满足这个均值是常数,自相关函数仅与时间间隔有关即可。
性质
遍历性
随机过程随便揪住一个实现,他就能在时间上经历随机过程的所有可能。
换个形象法的描述就是,在某一不变环境下打开开关一直不关,产生的随机信号中蕴含全部的信息。
这个就很好,可以用时间的特性来代替统计特性,不需要再知道这个随机过程的分布函数了,求什么平均就可以用时间平均代替统计平均。
注意这个遍历过程一定是平稳的,但是平稳不一定就是遍历,这两个并非互为充要关系。
后记
实平稳随机过程的自相关函数有一些性质,这里也不细讲了,做题的时候再说。


以及其有一些功率谱密度的计算:



高斯随机过程
定义
若随机过程的任意n维分布都是正态分布,则将其称为高斯随机过程或正态过程,
重要性质
高斯过程的n维分布完全由n个随机变量 \(x_1, x_2, \cdots, x_n\) 的数学期望、方差以及两两变量之间的归一化协方差函数决定;
广义平稳的高斯过程也狭义平稳;
高斯过程在不同时刻取值不相关,则它们也统计独立:
\[f_n(x_1, x_2, \cdots, x_n; t_1, t_2, \cdots, t_n) = f(x_1, t_1) f(x_2, t_2) \cdots f(x_n, t_n) \]
对于高斯变量来说,不相关和独立是等价的;
高斯过程经过线性变换(或线性系统)后仍为高斯过程,但数字特征发生改变;
若干个高斯过程的代数和仍为高斯过程,但数字特征发生改变:
若
\[X_1 \sim N(\mu_1, \sigma_1^2) , X_2 \sim N(\mu_2, \sigma_2^2) \]
,则
\[aX_1 + bX_2 \sim N(a\mu_1 + b\mu_2, a^2\sigma_1^2 + b^2\sigma_2^2) \]
还有两页PPT的内容,在这里直接略。
窄带随机过程
随机过程通过以 \(f_c\) 为中心频率的窄带系统的输出,即是窄带过程。
所谓窄带系统,是指其通带宽度 \(\Delta f<<f_c\) ,且 \(f_c\) 远离零频率的系统。
实际中,大多数通信系统都是窄带型的,通过窄带系统的信号或噪声必是窄带的,如果这时的信号或噪声又是随机的,则称它们为窄带随机过程。
如用示波器观察一个实现的波形,则如图2—4所示,它是一个频率近似为 \(f_c\) ,包络和相位随机缓变的正弦波。(注意是缓慢变化,这样基带信号带宽才窄)
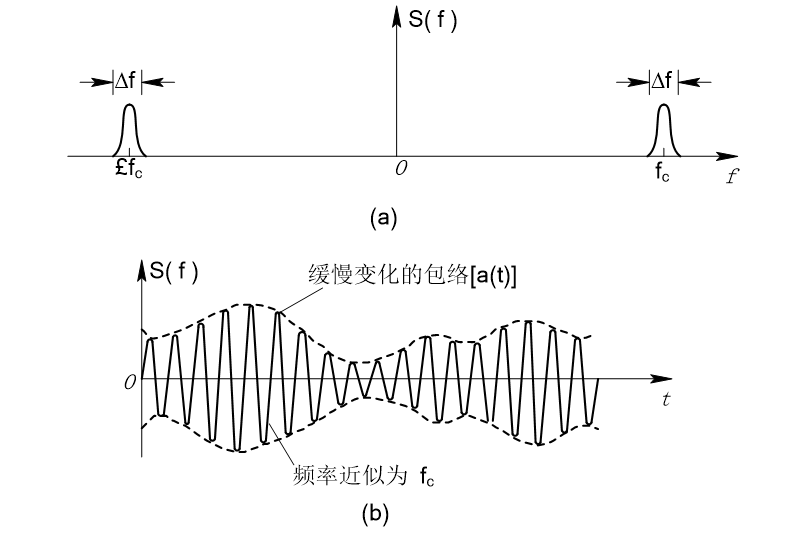
正弦波加窄带高斯过程
这个属于上面几部分的一个应用:
有个常用调制方法,就是拿正弦波(最简单的波)作为载波,接收机就是接受正弦已调信号和窄带高斯噪声的混合波形。
高斯白噪音和带限白噪音
定义
功率谱密度在所有频率上均为常数的噪声,即
双边功率谱密度: \(P_n(f) = \frac{n_0}{2} (-\infty < f < +\infty )\)
单边功率谱密度: \(P_n(f) = n_0 (0 < f < +\infty)\)
式中 \(n_0\) — 正常数
白噪声的自相关函数:对双边功率谱密度取傅里叶反变换,得到相关函数:
\[ R(\tau) = \frac{n_0}{2} \delta(\tau)\]