第五章 模拟调制系统
调制(Modulation)的定义与目的
把消息信号 \(m(t)\) 寄托在载波(\(\cos(\omega_c t)\))的某个参数上,形成已调信号。
目的
提高天线辐射效率:就是实现频谱的搬移。低频信号波长长,需要巨大天线;高频信号波长短,天线尺寸合理。
实现频谱资源共享:不同信号占据不同频段(频分复用FDM),实现多路通信。
提高系统抗干扰能力:非线性调制(如FM)可改善信噪比。
载波信号
本书中主要讲正弦波调制,脉冲调制暂时先不讲,后面可能有。
载波信号通常表示为:
\[ c(t) = A_c \cos(\omega_c t + \phi_c) \]
其中 \(A_c\) 为载波振幅,\(\omega_c\) 为载波角频率,\(\phi_c\) 为载波初始相位。调制即让 \(A_c\)、\(\omega_c\) 或 \(\phi_c\) 随基带信号 \(m(t)\) 变化。
模拟调制分类
幅度调制 (Amplitude Modulation, AM):载波振幅随 变化。即线性调制。
- DSB(双边带)
- AM(普通调幅)
- SSB(单边带)
- VSB(残留边带)
角度调制 (Angle Modulation, PM/FM):载波相位或频率随 \(m(t)\) 变化。
- FM(频率调制)
- PM(相位调制)
线性调制系统(幅度调制)
线性调制是将基带信号 \(m(t)\) 线性地作用于载波振幅。调制信号的时域表示为:
\[ s_{AM}(t) = A(t) \cos(\omega_c t) \]
幅度调制器的一般模型为:
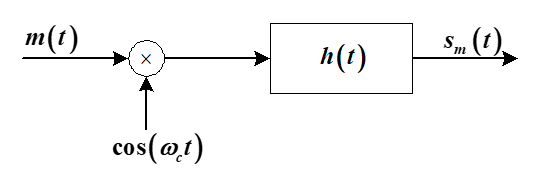
其分类就是根据这个 \(m(t)\) \(h(t)\) 不同来分的。
 ## 普通调幅 (AM)
## 普通调幅 (AM)
时域表达式
AM 信号在 DSB 基础上增加了载波分量:
\[ s_{AM}(t) = [A_0 + m(t)] \cos(\omega_c t) \]
其中 \(A_0\) 为直流偏置,必须满足 \(A_0 > |m(t)|_{max}\),以保证 \([A_0 + m(t)] > 0\)(不发生过调幅)。
调制指数 (\(\mu\))
\[ \mu = \frac{|m(t)|_{max}}{A_0} \le 1 \]
大于一为过调制,会导致失真、信息丢失。
功率和效率
AM 信号的总功率 \(P_{AM} = P_c + P_{SB}\)。边带功率 \(P_{SB}\) 承载信息,而载波功率 \(P_c\) 不承载信息。
- 效率:\(\eta = \frac{P_{SB}}{P_c + P_{SB}}\),AM 的效率通常很低,毕竟要满足调制系数不能大于1,他的载波功率是要比边带功率大的。
解调方法
可直接非相干解调 (Non-coherent Demodulation),使用包络检波器 (Envelope Detector),就一个二极管一个电容的事儿,电路简单,无需同步载波。
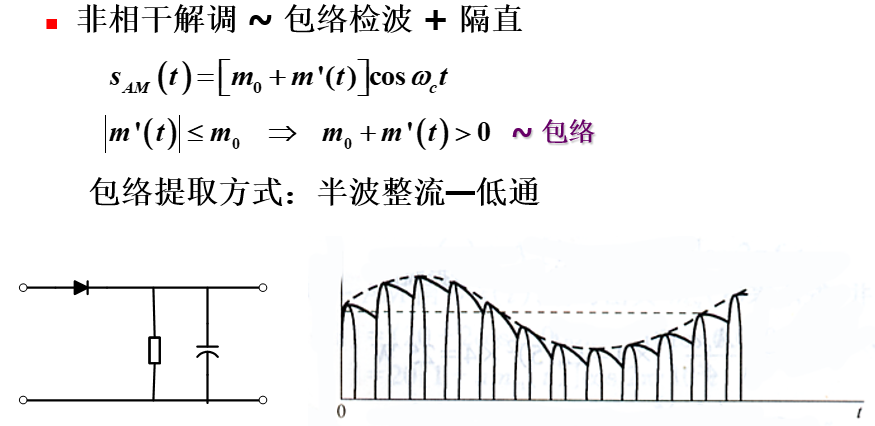
相干解调也可以,相对复杂,但是载波给了,还比较容易相干解调,记得解调完还需要去掉直流
双边带抑制载波 (DSB-SC)
时域表达式
无载波分量
\[ s_{DSB}(t) = m(t) \cos(\omega_c t) \]
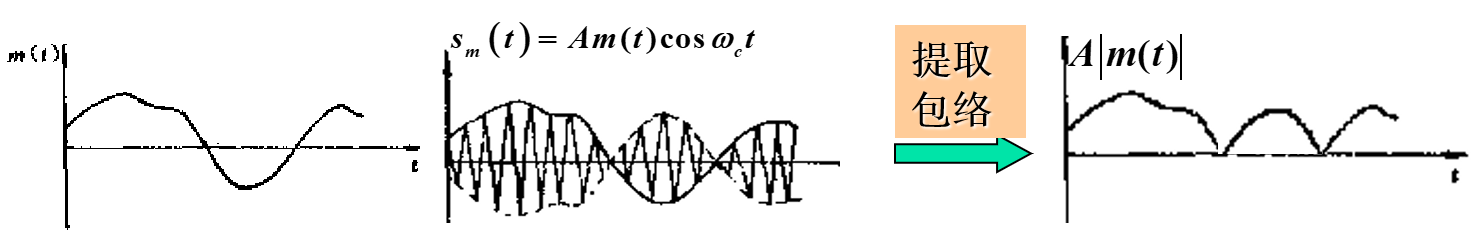
注意,这个载波和输入信号同时改变极性的时候会出现反向点。
频域特性
DSB 信号的频谱是基带信号 \(M(\omega)\) 频谱的左右平移:
\[ S_{DSB}(\omega) = \frac{1}{2} [M(\omega - \omega_c) + M(\omega + \omega_c)] \]
- 带宽:\(B_{DSB} = 2f_H\) (其中 \(f_H\) 为基带信号的最高频率)。
- 无载波分量。
- 幅值变为一半。
解调方法
关于相关解调和非相关解调之间的区别:
(1)相干解调信噪比可低于0dB;
(2)非相干解调信噪比需大于10dB ;
(3)相干解调的信噪比性能优于非相干解调,而非相干解调对移动、大动态信噪比环境下的适应性更好。
首先介绍相干解调:
接收端需要一个与载波同频同相的本地载波 \(\cos(\omega_c t)\):
他传来的信号里面没有载波分量,就需要我们揪出来一个。什么时候才能出频域分量?非线性变化。于是引入相乘:
- 相乘:
\[r(t) = s_{DSB}(t) \cdot 2\cos(\omega_c t) = m(t) \cos^2(\omega_c t) = m(t) [1 + \cos(2\omega_c t)]\]
\[ r(t) = m(t) + m(t) \cos(2\omega_c t) \]
- 低通滤波 (LPF):滤除高频项 \(m(t) \cos(2\omega_c t)\),得到 \(m(t)\)。实际上就是再给相干的分量乘进去,再滤除掉这个高频部分。
非相干上面讲过了,不再说。
单边带调制 (SSB)
频谱特性
SSB 只保留上边带 (USB) 或下边带 (LSB) 中的一个,极大地节省了带宽,并提高了功率效率。
但是由于理想滤波器不存在,频域法(LPF)做SSB很复杂,效果也就那样,当然也可以用相位法来进行抵消,也很复杂。
普通调幅接收机不能接受SSB信号,因为普通的只能做包络检波,不能做相干。
- 带宽:\(B_{SSB} = f_H\)。
时域表达式
\[ s_{SSB}(t) = m(t) \cos(\omega_c t) \mp \hat{m}(t) \sin(\omega_c t) \]
其中 \(\hat{m}(t)\) 是 \(m(t)\) 的希尔伯特变换。希尔伯特变换就是正余弦相移一个二分之pi。-可以看作上边带信号,+为下边带信号。
解调方法:相干解调
SSB 只能使用相干解调。(这个是为什么?)
残留边带调制 (VSB)
频谱特性
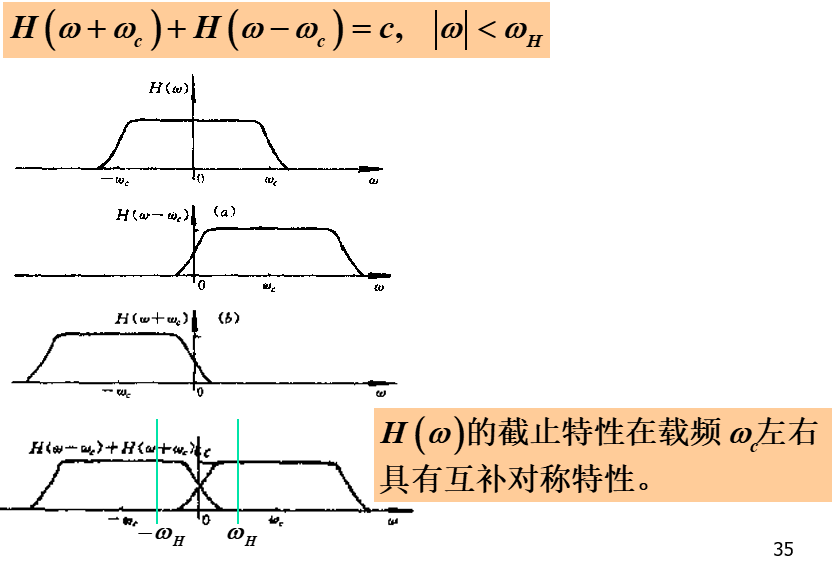
满足这个滤波器的截止特性在在载频处具有互补对称的条件就可以。
VSB 保留了一个完整的边带,以及另一边带的部分(残留边带)。是介于 DSB 和 SSB 之间的一种折中方案。
- 带宽:\(f_H < B_{VSB} < 2f_H\)。 ### 优势
VSB 解决了 SSB 难以实现的滤波器问题,并保留了低频分量,适用于传输带有丰富低频分量(如直流分量)的信号,例如电视信号。
解调方法:相干解调
角度调制系统(非线性调制)
这个我们不考,所以就只讲一点。基本上知道FM PM是啥,知道他们是非线性调制,出现了很多频域分量,带宽变大,出来的信号质量更好就行了。
角度调制是非线性调制,载波的瞬时相位或瞬时频率随基带信号 \(m(t)\) 变化。
调频 (Frequency Modulation, FM)
瞬时频率
载波的瞬时频率 \(\omega_i(t)\) 随 \(m(t)\) 线性变化: \[ \omega_i(t) = \omega_c + k_f m(t) \] 其中 \(k_f\) 为调频系数,单位为 \(\text{rad/s/V}\)。 ### 时域表达式 \[ s_{FM}(t) = A_c \cos[\omega_c t + \phi(t)] \] 瞬时相位 \(\phi(t)\) 是瞬时频率对时间的积分: \[ \phi(t) = \int^t \omega_i(\tau) d\tau = \omega_c t + k_f \int^t m(\tau) d\tau \] FM 信号: \[ s_{FM}(t) = A_c \cos[\omega_c t + k_f \int^t m(\tau) d\tau] \]
调制指数 (\(\beta\))
对于单音调制 \(m(t) = A_m \cos(\omega_m t)\),FM 信号的调制指数为: \[ \beta = \frac{\Delta \omega}{\omega_m} = \frac{k_f A_m}{\omega_m} \] 其中 \(\Delta \omega = k_f A_m\) 为最大角频偏。
带宽(卡森公式)
FM 信号的频谱是无限宽的,但能量主要集中在有限带宽内。卡森 (Carson) 公式用于估算有效带宽: \[ B_{FM} \approx 2(\Delta f + f_m) = 2(\beta + 1) f_m \] 其中 \(\Delta f\) 为最大频偏(赫兹)。
解调方法
FM 信号通常采用鉴频器 (Frequency Discriminator) 来解调,它将频率变化转换为幅度变化,再进行包络检波或低通滤波。
调相 (Phase Modulation, PM)
瞬时相位
载波的瞬时相位 \(\theta_i(t)\) 随 \(m(t)\) 线性变化: \[ \theta_i(t) = \omega_c t + k_p m(t) \] 其中 \(k_p\) 为调相系数。 ### 时域表达式 \[ s_{PM}(t) = A_c \cos[\omega_c t + k_p m(t)] \]
FM 与 PM 的关系
- 对 \(m(t)\) 进行积分后对载波进行 FM 调制,得到 PM 信号。
- 对 \(m(t)\) 进行微分后对载波进行 PM 调制,得到 FM 信号。
模拟调制系统的抗噪声性能
通信系统的抗噪声性能通常由解调器的抗噪声性能来衡量。在信道加性高斯白噪声的背景下,研究各种调制系统的性能。
性能分析模型与指标
接收机模型
已调信号 \(s_m(t)\) 与信道加性高斯白噪声 \(n(t)\) 混合后,先经过带通滤波器 (BPF) 滤除信号频带外的噪声,输入到解调器的信号为 \(s_m(t)\),噪声为 \(n_i(t)\)。解调器输出的有用信号为 \(m_o(t)\),噪声为 \(n_o(t)\)。
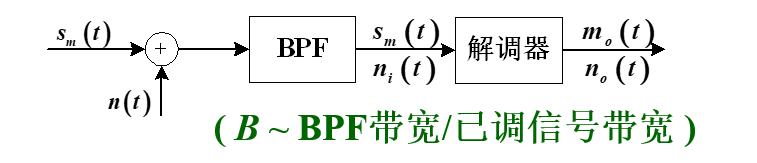
输入端噪声特性
输入解调器的噪声 \(n_i(t)\) 是由平稳高斯白噪声 \(n(t)\) 经过带通滤波器得到的,可视为平稳窄带高斯噪声。
窄带高斯噪声可以表示为:
\[ n_{i}(t)=n_{c}(t)\cos\omega_{c}t-n_{s}(t)\sin\omega_{c}t \]
其中 \(n_c(t)\) 和 \(n_s(t)\) 分别是同相分量和正交分量,均值都为 \(0\),且具有相同的方差。
输入噪声功率:若白噪声单边功率谱密度为 \(N_0\),BPF 带宽为 \(B\) (等于已调信号带宽 \(W\)):
\[ N_{i}=\overline{n_{i}^{2}(t)}=N_{0}B \]
质量指标
输出信噪比 (Output SNR):衡量解调器输出的质量。
\[ \frac{S_{o}}{N_{o}}=\frac{\overline{m_{o}^{2}(t)}}{\overline{n_{o}^{2}(t)}} \]
输入信噪比 (Input SNR):
\[ \frac{S_{i}}{N_{i}}=\frac{\overline{s_{m}^{2}(t)}}{\overline{n_{i}^{2}(t)}} \]
调制制度增益 (Gain):用于比较同类调制系统的性能。
\[ G=\frac{S_{o}/N_{o}}{S_{i}/N_{i}} \]
线性调制系统性能推导
1. DSB-SC 调制系统 (相干解调)
输入信号功率:\(S_{i} = \overline{s_{DSB}^{2}(t)} = \frac{1}{2}\overline{m^{2}(t)}\)。
输出信号:\(m_{o}(t)=\frac{1}{2}m(t)\)。
输出信号功率:\(S_{o} = \overline{m_{o}^{2}(t)} = \frac{1}{4}\overline{m^{2}(t)}\)。
输出噪声功率:\(N_{o} = \frac{1}{4}\overline{n_{i}^{2}(t)} = \frac{1}{4}N_{0}B\)。
调制制度增益:\(G_{DSB} = 2\)。
2. SSB-SC 调制系统 (相干解调)
带宽:\(B=W\) (基带信号带宽)。
输出信号功率:\(S_{o}=\overline{m_{o}^{2}(t)}=\frac{1}{16}\overline{m^{2}(t)}\)。
输出噪声功率:\(N_{o} = \frac{1}{4}N_{0}W\)。
调制制度增益:\(G_{SSB} = 1\)。
3. DSB 与 SSB 性能比较
虽然 \(G_{DSB}=2\) 且 \(G_{SSB}=1\),但这并不直接说明 DSB 性能更好。因为两者输入信号功率和带宽不同。
结论:在相同的输入信号功率 \(S_i\)、相同的噪声功率谱密度 \(N_0\)、相同的基带信号带宽 \(W\) 条件下,DSB 和 SSB 的输出信噪比相等,表明两者的抗噪声性能是相同的。
4. AM 包络检波的性能
大信噪比情况:包络检波的性能与相干解调相同。
小信噪比情况:出现门限效应。在小信噪比下,包络检波器会把有用信号扰乱成噪声,输出信噪比急剧恶化。
各种模拟调制系统的性能比较
| 调制方式 | 传输带宽 | 直流响应 | 设备复杂性 | 主要应用 |
|---|---|---|---|---|
| DSB | \(2f_H\) (无) | 无 | 中等:要求相干解调 | 模拟数据传输 |
| AM | \(2f_H\) (有) | 有 | 较小:调制与解调简单 | 无线电广播 |
| SSB | \(f_H\) (无) | 无 | 较大:要求相干解调,调制器也较复杂 | 话音通信,话音频分多路通信 |
| VSB | \(f_H < B < 2f_H\) (有) | 有 | 较大:要求相干解调,调制器需要对称滤波 | 数据传输,宽带(电视)系统 |
| FM | \(2(\Delta f + f_m)\) (有) | 有 | 中等:调制器有点复杂,解调器较简单 | 数据传输,无线电广播,微波中继 |
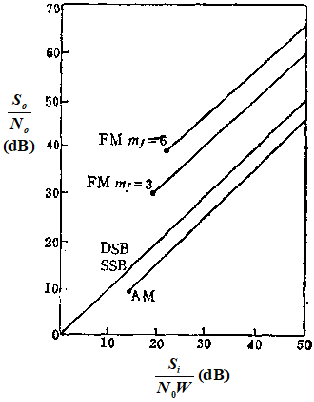
主要结论
抗噪声性能:WBFM (宽带调频) 最好;DSB、SSB、VSB 次之;AM 最差。当输入信噪比较高时,FM 的调频指数 \(\beta\) 越大,抗噪声性能越好。
频带利用率:SSB 的带宽最窄,\(B_{SSB}=f_H\),频带利用率最高。FM 占用带宽最大,随调频指数 \(\beta\) 增大而增大,频带利用率最低。
权衡:FM 是以牺牲有效性(带宽)来换取可靠性(抗噪声性能)的典型代表。
频分复用 (FDM)
概念与目的
复用 (Multiplexing):解决如何利用一条物理信道同时传输多路信号的技术。目的是为了充分利用信道的频带、时间、空间资源,提高信道的利用率。
频分复用 (FDM):是一种按频率来划分信道的复用方式。
FDM 原理与实现
划分频段:将信道的总带宽划分为多个相互不重叠的频段(子通道),每路信号占据其中一个子通道。
保护频带:各路信号之间留有未被使用的频带(保护频带)进行分隔,以防止信号重叠和路间干扰。
发送端:每路基带信号 \(m_i(t)\) 先经过低通滤波 (LPF),然后与不同的载波 \(\omega_{c_i}\) 相乘(调制),再经过边带滤波器 (\(\text{SBF}_i\)) 选出所需的边带,最后通过相加器将多路已调信号合路并送入信道。
接收端:接收到的合路信号经过带通滤波器 (\(\text{BPF}_i\)) 分离出对应的子通道信号,再与同频载波 \(\omega_{c_i}\) 相乘(解调),最后经过 LPF 即可恢复出原始基带信号 \(m_i(t)\)。
FDM 优缺点
优点:
信道复用率高。
允许复用的路数多。
分路(分频)方便。
缺点:
设备生产较为复杂。
滤波器特性不理想和信道内存在非线性会产生路间干扰。