第一章 概率论基础
这是正文
1.1 基本概念
随机试验 (Random Experiment):结果不可预知,但可重复。
样本空间 \(\Omega\):所有可能结果的集合。
随机事件 \(A \subseteq \Omega\):
基本事件:仅含一个结果;
复合事件:多个结果;
\(\Omega\) 为必然事件,\(\varnothing\) 为不可能事件。
概率(公理化定义)
\(0 \le P(A) \le 1\)
\(P(\Omega) = 1\)
若 \(A \cap B = \varnothing\),则 \(P(A \cup B) = P(A) + P(B)\)
注:古典概率 / 几何概率 / 频率概率 / 公理化概率只是不同理解方式,本课程采用公理化定义 + 密度函数形式化处理。

1.2 一维随机变量
定义
随机变量 \(X(\omega)\):是从样本空间映射到实数域的函数。
分布函数
\[F_X(x) = P\{X \le x\}\]
性质:
- 单调非减;
- 右连续;
- \(\lim_{x\to -\infty}F=0\),\(\lim_{x\to +\infty}F=1\)
离散型与连续型
| 类型 | 描述 | 表征方式 |
|---|---|---|
| 离散型 | \(P\{X=x_k\}=p_k\) | 概率质量函数 (PMF) |
| 连续型 | \(P\{x<X<x+dx\}=f(x)dx\) | 概率密度函数 (PDF) |
离散型的 PDF 也可用 Dirac 函数统一:
\[f(x) = \sum_k p_k \delta(x - x_k)\]

随机变量函数变换
若 \(Y = g(X)\):
- 单调可逆:
\[f_Y(y) = f_X(x) \left| \frac{dx}{dy} \right|\]
具体推导方式就是:
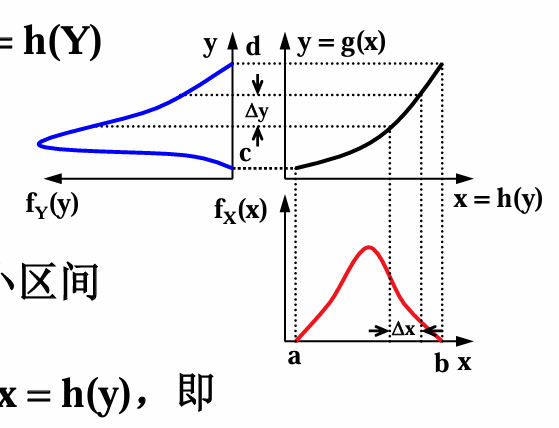
看这个图,如果要求这个y的分布的话,直接拿这个 \(\Delta y\) 和 \(\Delta x\) 的比值就是这个 y 和 x 的比值来算
- 非单调可逆:多个解累加。
常见例子:\(Y = \sin X\)、\(Y = X^2\) 等。
这个题的话,等会看看作业里面有没有,ppt上的题不是很清楚。
1.3 多维随机变量
联合分布函数
\[F_{XY}(x,y) = P\{X \le x, Y \le y\}\]
联合密度函数
\[f_{XY}(x,y) = \frac{\partial^2 F_{XY}}{\partial x \partial y}\]
边缘分布
边缘分布的意思就是不考虑其中一个因素,只考虑另外一个因素。
\[f_X(x) = \int_{-\infty}^{+\infty} f_{XY}(x,y) \, dy\]
条件密度
\[f_{Y|X}(y|x) = \frac{f_{XY}(x,y)}{f_X(x)}\]
若 \(f_{XY}(x,y) = f_X(x)f_Y(y)\),则称 独立。
二维随机变量变换(Jacobian)
若
\[ Y_1 = g_1(X_1,X_2), \quad Y_2 = g_2(X_1,X_2) \]
则
\[ f_{Y_1Y_2}(y_1,y_2) = f_{X_1X_2}(x_1,x_2) \cdot \left| J_g^{-1} \right| \]

1.4 数字特征
一维
| 名称 | 离散 | 连续 |
|---|---|---|
| 期望 | \(E[X]=\sum x_k p_k\) | \(E[X]=\int xf(x)dx\) |
| 方差 | \(D[X]=E[X^2]-E[X]^2\) | 同左 |
二维
- 协方差
\[\mathrm{cov}(X,Y) = E[XY] - E[X]E[Y]\]
- 相关系数
\[\rho_{XY} = \frac{\mathrm{cov}(X,Y)}{\sqrt{D[X]D[Y]}}\]
- 性质:\(\rho \in [-1,1]\),\(|\rho|\) 越大,线性相关性越强。
1.5 特征函数
\[\phi_X(u) = E[e^{juX}]\]
- 相当于 \(f_X(x)\) 的傅里叶变换;
- 可用于推导卷积、证明极限定理;
- 高斯分布的特征函数仍为高斯型。
1.4 随机变量的数字特征
一维随机变量
| 名称 | 离散型 | 连续型 |
|---|---|---|
| 期望 | \(E[X]=\sum x_k p_k\) | \(E[X]=\int xf(x)dx\) |
| 方差 | \(D[X]=E[X^2]-E[X]^2\) | 同左 |
| 原点矩 | \(\mu_k=E[X^k]\) | 同左 |
| 绝对矩 | \(\lambda_k=E[\|X\|^k]\) | 同左 |
| 中心矩 | \(v_k=E[(X-E[X])^k]\) | 同左 |
| 标准矩 | \(\tilde{v}_k=E\left[\left(\frac{X-\mu_X}{\sigma_X}\right)^k\right]=\frac{v_k}{\sigma_X^k}\) | 同左 |
数字特征性质
函数期望:\(E[g(\xi)]=\int g(x)f(x)dx\)
线性:\(E[a\xi+b]=aE[\xi]+b\)
方差:\(D[a\xi+b]=a^2D[\xi]\)
中心矩与原点矩关系:
\[v_n=\sum_{k=0}^n(-1)^{n-k}C_n^k\mu_1^{n-k}\mu_k\]
- 最小方差性:\(E[(\xi-E[\xi])^2]\leq E[(\xi-x)^2]\)
二维随机变量
| 名称 | 离散型 | 连续型 |
|---|---|---|
| 联合原点矩 | \(E[X^jY^k]=\sum\sum x_m^j y_n^k p_{m,n}\) | \(E[X^jY^k]=\iint x^j y^k f(x,y)dxdy\) |
| 联合中心矩 | \(E[(X-E[X])^j(Y-E[Y])^k]\) | 同左 |
| 相关 | \(R_{XY}=E[XY]\) | 同左 |
| 协方差 | \(K_{XY}=E[XY]-E[X]E[Y]\) | 同左 |
| 相关系数 | \(r_{XY}=\frac{K_{XY}}{\sigma_X\sigma_Y}\) | 同左 |
重要概念
- 协方差矩阵:
\[\Sigma=\begin{bmatrix}K_{XX} & K_{XY}\\ K_{YX} & K_{YY}\end{bmatrix}\]
- 不相关:\(r_{XY}=0 \Leftrightarrow K_{XY}=0 \Leftrightarrow E[XY]=E[X]E[Y]\)
相互独立则不相关,反之不相关不一定相互独立,因为相关性描述的只是两个随机变量的线性相关程度,比是否真正的独立无关。独立要比不相关要强一些。但对于联合正态分布,不相关与统计独立等价。
- 正交:\(E[XY]=0\),若XY有一方均值为0,则XY不相关与XY正交等价。
线性最小均方估计
最优线性估计:\(\hat{Y}=E[Y]+\frac{K(X,Y)}{D(X)}(X-E[X])\)
最小均方误差:\(\min e=(1-r_{XY}^2)D(Y)\)
1.5 随机变量的特征函数
定义
实际上就是fourier变换。
\[C(u)=E[e^{juX}]=\int_{-\infty}^{\infty}e^{jux}f(x)dx\]
性质
有界性:\(|C(u)|\leq C(0)=1\)
共轭对称:\(C(-u)=\overline{C(u)}\)
线性变换:若\(Y=aX+b\),则\(C_Y(u)=e^{jub}C_X(au)\)
矩生成:\(E[X^k]=j^{-k}C^{(k)}(0)\)
独立性:若\(X,Y\)独立,则\(C_{X+Y}(u)=C_X(u)C_Y(u)\)
高斯分布特征函数
- \(X\sim N(a,\sigma^2)\)的特征函数:
\[C_X(u)=\exp\left(jau-\frac{\sigma^2 u^2}{2}\right)\]
高斯随机变量的线性变换仍为高斯分布
多维情况:若\(X\sim N(m_X,K_X)\),则\(Y=AX+b\sim N(Am_X+b,AK_XA^T)\)