第二章 随机过程-时域分析

1 随机过程的基本概念及其统计特性

1.1 随机过程的基本概念

随机过程 \(X(t,s)\) 可以从宏观和微观两个角度理解：

视角	描述	固定项	变量项	结果
宏观（时间函数族）	样本空间到函数空间的映射	无固定	\(t\) 和 \(s\) 都是变量	随机过程
样本函数	随机过程的一次实现	\(s\) 固定	\(t\) 是变量	确知时间函数
微观（时变随机变量）	对于每个特定时间 \(t_i\)，它都是随机变量	\(t\) 固定	\(s\) 是变量	随机变量
确定值	样本点和时间都固定	\(t\) 和 \(s\) 都固定	无变量	确定值

**定义1（时间函数族/宏观）：

设随机实验的样本空间 \(S=\{s_i\}\)，对于空间的每个样本 \(s_i \in S\)，总有一个时间函数 \(X(t,s_i)\) 与之对应 (\(t \in T\))，空间的所有样本 \(S=\{s_i\}\) 对应一族时间函数 \(\{X(t,s_i), s_i \in S\}\)，则样本空间到函数空间的映射称为随机过程。

**定义2（时变随机变量/微观）：

对于每个特定的时间 \(t_i\)，\(X(t_i,s)\) 都是随机变量，则称 \(X(t,s)\) 为随机过程。

这个在通信原理实际上已经明白了，不再细讲。

1.2 随机过程的分类

一、按时间和幅度（状态）连续/离散

• 连续型随机过程： 时间连续，状态连续。
• 离散型随机过程： 时间连续，状态离散。
• 连续随机序列： 时间离散，状态连续。
• 离散随机序列： 时间离散，状态离散。

一堆废话，不用看。

二、按样本函数的性质

• **不确定（不可预测）随机过程

• 确定（可预测）随机过程：如随机相位信号 \(A\sin(\omega t+\Phi), \Phi \sim U(0,2\pi)\)。

三、按概率分布的特性

• 平稳随机过程： 统计特性不随时间变化的，如热噪声。
• 正态随机过程
• 马尔科夫随机过程
• 独立增量过程
• 独立随机过程

不用细看，只要有这样的分类就行，没啥用。

1.3 随机过程的概率分布

“随机”中的“确定”是指用统计平均值（矩、特征函数、概率分布/密度函数）来描述随机过程的整体特性。

一、一维概率分布

• 一维分布函数： \(F_X(x;t) = P\{X(t) \le x\}\)（是确定函数）。

• 一维概率密度： \(f_X(x;t) = \frac{\partial F_X(x;t)}{\partial x}\)（可能是时变概率密度）。

二、二维概率分布

• 二维分布函数： \(F_{X_1X_2}(x_1,x_2;t_1,t_2) = P\{X(t_1) \le x_1, X(t_2) \le x_2\}\)。

• 二维概率密度： \(f_{X_1X_2}(x_1,x_2;t_1,t_2) = \frac{\partial^2 F_{X_1X_2}(x_1,x_2;t_1,t_2)}{\partial x_1 \partial x_2}\)。

三、利用随机变量变换求概率密度函数

• 单调可逆变换： \(Y = g(X), X = h(Y)\)

  \[f_Y(y) = f_X[x=h(y)] \left| \frac{dh(y)}{dy} \right| = f_X(x) \left| \frac{dg(x)}{dx} \right|^{-1} \Big|_{x=h(y)}\]

• 非单调可逆变换： \(Y = g(X)\)，有多个根 \(X_k = h_k(Y)\)

  \[f_Y(y) = \sum_{k} f_X[x=h_k(y)] \left| \frac{dh_k(y)}{dy} \right|\]

• 二维变换（Jacobian行列式）： \(Y_1=g_1(X_1,X_2), Y_2=g_2(X_1,X_2)\)

  \[f_{Y_1Y_2}(y_1,y_2) = \left| J_h(y_1,y_2) \right| f_{X_1X_2}[x_1=h_1(y_1,y_2), x_2=h_2(y_1,y_2)]\]

  其中 \(|J_h|\) 是 \(X_1, X_2\) 对 \(Y_1, Y_2\) 的偏导数构成的行列式绝对值。

第一章讲差不多了，这里不再细说。

1.4 随机过程的数字特征

• 均值函数 \(m_X(t) = E[X(t)]\)

注：也叫二阶原点矩

• 方差函数 \(D_X(t) = E\{[X(t)-m_X(t)]^2\}\)

注：也叫二阶中心矩

• 自相关函数 \(R_X(t_1, t_2) = E[X(t_1)X(t_2)]\)

• 协方差函数 \(K_X(t_1, t_2) = R_X(t_1, t_2) - m_X(t_1)m_X(t_2)\)

2 随机过程的微分与积分

2.0 基础概念：均方极限

• 二阶矩过程： 满足 \(\forall t \in T, E[X^2(t)] < \infty\) 的随机过程。

• 均方极限（l.i.m.）： 称随机变量序列 \(\{X_n\}\) 均方收敛于 \(X\)，记为 \(\underset{n\rightarrow\infty}{\mathrm{l.i.m.}} X_n = X\)，此时：

  \[\lim_{n\rightarrow\infty} E|X_n - X|^2 = 0\]

其中l.i.m是英文limit in mean square的缩写

之所以定义一个均方收敛，其意义和普通的收敛不同，强调是他的均方会收敛到一个值，而不是所有的样本点会收敛到一个值。

当然，在做题上来说，实际上还是用求微积分的那一套罢了。

均方极限的性质

\[\underset{n \to \infty}{\text{l.i.m}} c_n = \lim_{n \to \infty} c_n = c\]

\[\underset{n \to \infty}{\text{l.i.m}} Z = Z \]

\[\underset{n \to \infty}{\text{l.i.m}} c_n Z = cZ\]

• 运算性： 均方极限与加法、常数乘法、期望（\(E\)）的次序可交换。

  \[\underset{n \to \infty}{\text{l.i.m}} (aX_n + bY_n) = aX + bY\]

  \[\lim_{n\rightarrow\infty} E X_n = E X = E \left[ \lim_{n\rightarrow\infty} X_n \right]\]

• 均方收敛判定准则（Cauchy准则）： \(\{X_n\}\) 均方收敛的充要条件是：

  \[\lim_{n,m\rightarrow\infty} E|X_m - X_n|^2 = 0\]

2.1 随机连续性：均方连续

• 定义： 称 \(X(t)\) 在时刻 \(t_0\) 均方连续，如果：

  \[\lim_{\Delta t\rightarrow0} E\{[X(t_0+\Delta t)-X(t_0)]^2\} = 0\]

• 均方连续准则（充要条件）：

  二阶矩过程 \(X(t)\) 在 \(t_0\) 处均方连续的充要条件为：相关函数 \(R(s,t)\) 在 \((t_0, t_0)\) 处连续。

  （二阶矩过程的均方连续性可用它的相关函数的普通连续性来确定。）

• 性质：

  • 若 \(X(t)\) 在 \(t_0\) 处均方连续，则其均值函数 \(m_X(t)\) 和方差函数 \(D_X(t)\) 也在 \(t_0\) 处连续。

  • “E” 和 “l.i.m.” 次序可换。

2.2 随机过程的微分（均方可微）

• 均方可微准则（充要条件）：

  二阶矩过程 \(X(t)\) 在 \(t_0\) 处均方可微的充要条件为：相关函数 \(R(s,t)\) 在 \((t_0, t_0)\) 处广义二阶可微。用人话来说就是相关函数在它的自变量相等时，存在二阶混合偏导数且连续。

• 均方导数的性质：

  • 若 \(X(t)\) 在 \(t\) 处均方可微，则 \(X(t)\) 在 \(t\) 处均方连续。

  • “E” 和 “\(\frac{d(\cdot)}{dt}\)” 次序可交换。 即 \(E[\frac{d}{dt}X(t)] = \frac{d}{dt}E[X(t)]\)。

2.3 随机过程的积分（均方可积）

• 均方可积充分条件：

  • 对于二阶矩过程 \(X(t)\)，若其相关函数 \(R(s,t)\) 的二重积分存在且有限，则 \(X(t)\) 在 \([a,b]\) 上均方可积。

  • 若 \(X(t)\) 在 \([a,b]\) 上均方连续，则 \(X(t)\) 在 \([a,b]\) 上均方可积。

• 均方积分的性质：

  • “E” 与均方积分次序可换。 即 \(E[\int_a^b X(t)dt] = \int_a^b E[X(t)]dt\)。

3 平稳随机过程和遍历性过程

3.1 平稳随机过程

• 平稳随机过程： 统计特性不随时间的推移而变化的随机过程。

• 分为：严平稳（SSS） 和 宽平稳（WSS）。

一、严平稳随机过程（Strict-Sense Stationary, SSS）

• 定义： 随机过程 \(X(t)\) 的任意 \(n\) 维概率分布函数 \(F_X(x_1,\dots,x_n; t_1,\dots,t_n)\) 不随时间平移而变化，即与时间起点无关，只与时间差 \(\tau_k=t_k-t_1\) 有关。

  \[F_X(x_1,\dots,x_n; t_1,\dots,t_n) = F_X(x_1,\dots,x_n; t_1+\tau,\dots,t_n+\tau)\]

• 低阶矩特性：

  • 均值函数 \(m_X(t)\) 与时间 \(t\) 无关，为常数。

  • 自相关函数 \(R_X(t_1, t_2)\) 只与时间差 \(\tau=t_2-t_1\) 有关，即 \(R_X(\tau)\)。

但是很明显，这个条件过于的严苛，一般是到不了的，所以适用范围相对较窄，我们需要引入这个宽平稳来说事。

二、宽平稳随机过程（Wide-Sense Stationary, WSS）

• 定义（辛钦Khinchine）： 随机过程 \(X(t)\) 满足：

  1. 均值函数 \(m_X(t)\) 是一个与时间 \(t\) 无关的常数 \(m_X\)。

  2. 自相关函数 \(R_X(t_1, t_2)\) 只与时间差 \(\tau=t_2-t_1\) 有关，即 \(R_X(\tau)\)。

• 关系：

  • 严平稳 \(\implies\) 宽平稳（反之不成立，正态过程除外）。

• 性质：

这一部分说实在的没怎么看清楚看明白。

image.png

image.png

image.png

image.png

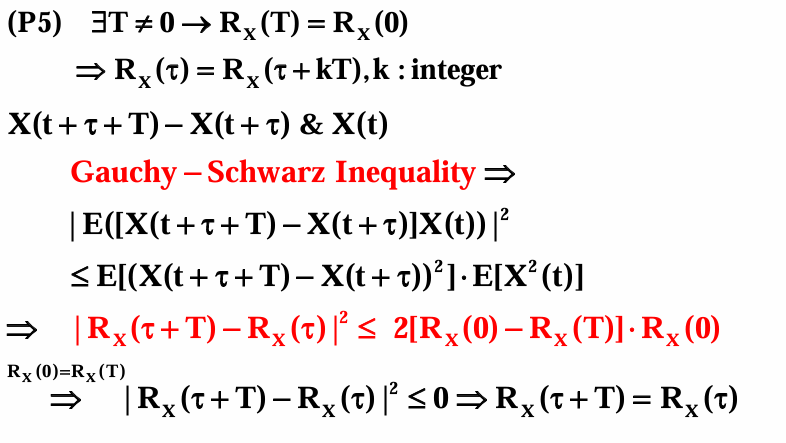
接着引入相关时间：

image.png

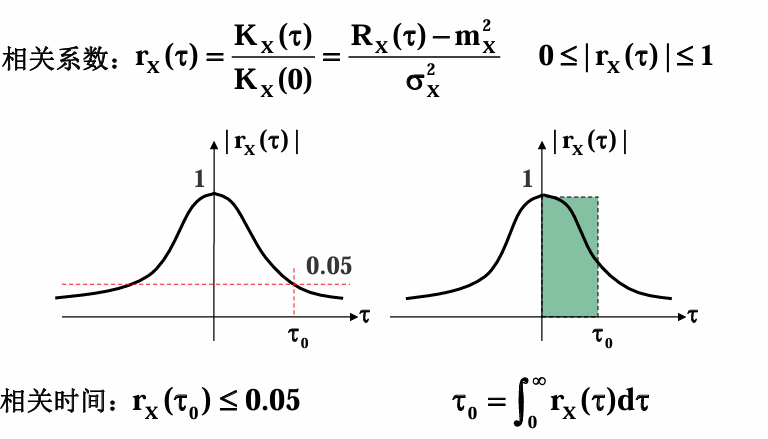
\(\tau_0\) 越小意味着相关系数随着 \(\tau\) 增加而衰落的更快，表明随机过程随着时间变化更剧烈。

3.2 循环平稳随机过程

作为补充

3.3 遍历性过程（Ergodicity）

就是将统计平均变为时间平均。

• 基本思想： 统计平均（对样本族求平均）等于时间平均（对单个样本函数求时间平均）。

  • 时间平均： 时间均值 \(\overline{X}\)、时间相关函数 \(\mathfrak{R}_X(\tau)\)。

• 宽遍历性过程的定义： 设随机过程 \(X(t)\) 为广义平稳，且同时满足均值和自相关函数的遍历性，则定义该随机过程为宽遍历性过程。

  1. 均值遍历性： 时间均值均方收敛于统计均值。

     \[\overline{X} = \lim_{T\rightarrow\infty} \frac{1}{2T} \int_{-T}^{T} X(t)dt \xrightarrow{\mathrm{m.s.}} E[X(t)]\]

  2. 自相关函数遍历性： 时间自相关函数均方收敛于统计自相关函数。

     \[\mathfrak{R}_X(\tau) = \lim_{T\rightarrow\infty} \frac{1}{2T} \int_{-T}^{T} X(t)X(t+\tau)dt \xrightarrow{\mathrm{m.s.}} R_X(\tau)\]

实际上就是直接看到平稳信号就直接用了，也不管他三七二十一，瞎几把用就得了。

4 随机过程的联合概率分布和互相关函数

4.1 两个随机过程的联合概率分布

设有两个随机过程 \(X(t)\) 和 \(Y(t)\)。

• \((n+m)\) 维联合分布函数：

  \[F_{XY}(x_1,\dots,x_n;y_1,\dots,y_m;t_1,\dots,t_n;t_1',\dots,t_m') = P\{X(t_1) \le x_1,\dots, X(t_n) \le x_n; Y(t_1') \le y_1,\dots, Y(t_m') \le y_m\}\]

• \((n+m)\) 维联合概率密度：

  \[f_{XY}(\dots) = \frac{\partial^{n+m}F_{XY}(\dots)}{\partial x_1 \dots \partial x_n \partial y_1 \dots \partial y_m}\]

• 注意：

  1. 若两个过程的 \(n+m\) 维联合概率分布给定，则它们的全部统计特性也确定了。

  2. 可由高维联合分布求出它们的低维联合概率分布。

没啥好讲的，就单纯上面已知的推广。

4.2 互相关函数

• 互相关函数定义： 描述两个随机过程在不同时刻状态之间的统计关联性。

  \[R_{XY}(t_1, t_2) = E[X(t_1)Y(t_2)] = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}xyf_{XY}(x,y;t_1,t_2)dxdy\]

• 互协方差函数（中心化互相关函数）： \[K_{XY}(t_1, t_2) = E\{[X(t_1)-m_X(t_1)][Y(t_2)-m_Y(t_2)]\}\] \[K_{XY}(t_1, t_2) = R_{XY}(t_1, t_2) - m_X(t_1)m_Y(t_2)\]

相互关系

关系	定义	互相关函数 \(R_{XY}(t_1, t_2)\)	互协方差函数 \(K_{XY}(t_1, t_2)\)
统计独立	\(f_{XY} = f_X f_Y\)	\(m_X(t_1)m_Y(t_2)\)	\(0\)
不相关	\(K_{XY}(t_1, t_2)=0\)	\(m_X(t_1)m_Y(t_2)\)	\(0\)
正交	\(R_{XY}(t_1, t_2)=0\)	\(0\)	\(-m_X(t_1)m_Y(t_2)\)

[!WARNING] 这个写的有点问题； 另外，CXZ是我儿

• 注意：

  1. 如果两个随机过程相互独立，且它们的二阶矩都存在，则必互不相关。

  2. 正态随机过程的不相关与相互独立等价。

不想学了听会歌 QAQ

<iframe width="100%" height="468" src="https://player.bilibili.com/player.html?bvid=BV1JThqzwEGq&p=1&autoplay=0" scrolling="no" border="0" frameborder="no" framespacing="0" allowfullscreen="true" &autoplay=0 >

联合平稳性

• 联合严平稳： \(X(t)\) 和 \(Y(t)\) 的联合概率分布不随时间平移而变化。

• 联合宽平稳（宽平稳相依）：

  1. \(X(t)\) 和 \(Y(t)\) 各自宽平稳。

  2. 互相关函数 \(R_{XY}(t, t+\tau)=R_{XY}(\tau)\)（只与时间差 \(\tau\) 有关）。

• 联合宽遍历：

  1. \(X(t)\) 和 \(Y(t)\) 联合宽平稳。

  2. 时间互相关函数均方收敛于统计互相关函数。

     \[\mathfrak{R}_{XY}(\tau) = \underset{T\rightarrow\infty}{\mathrm{l.i.m.}} \frac{1}{2T}\int_{-T}^{T}X(t)Y(t+\tau)dt = R_{XY}(\tau)\]

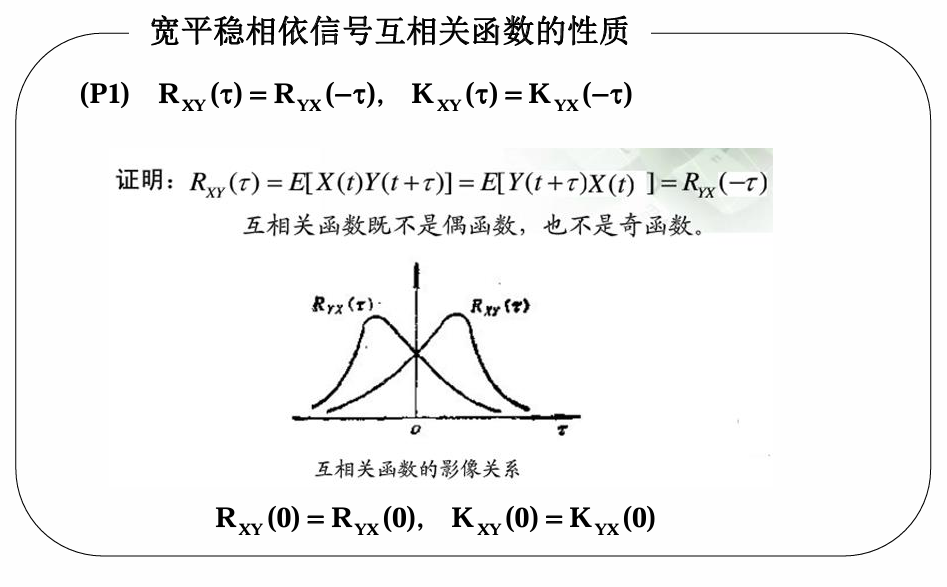
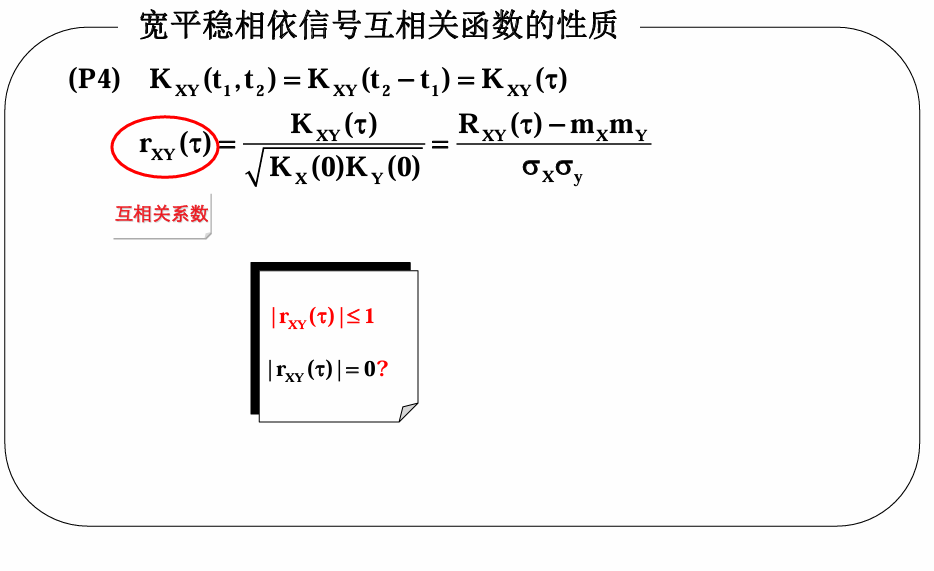
5 复随机过程

• 复随机信号： \(Z(t) = X_c(t) + jX_s(t)\)。

他的计算跟实随机过程的区别和复数与实数的区别一样的，这里不再赘述

• 宽平稳复随机过程：

  1. 均值函数 \(m_Z(t) = E[Z(t)]\) 是常数。

  2. 自相关函数 \(R_Z(t_1, t_2) = E[Z(t_1)Z^*(t_2)]\) 只与时间差 \(\tau=t_2-t_1\) 有关，即 \(R_Z(\tau)\)。

• 联合宽平稳复随机过程：

  1. \(Z_1(t)\) 和 \(Z_2(t)\) 各自宽平稳。

  2. 互相关函数 \(R_{Z_1Z_2}(t, t+\tau) = E[Z_1(t)Z_2^*(t+\tau)]\) 只与 \(\tau\) 有关。

[!NOTE] 可以看出，这个区别跟实数与复数的区别一样的，不用太细致的看。

6 离散时间随机过程

• 表示： \(X(nT)\) 或 \(X(n)\)。

• 分析方法： 本质上与连续时间随机信号的分析一样。

• 对应关系： 时间变量 \(t \rightarrow n\)。

[!NOTE] 可以看出，这个和连续时间的区别基本等于没有，不用太细致的看。

7 正态随机过程

高斯分布性质

image.png

• 主要性质：

  1. 正态随机过程的 \(n\) 维概率密度完全由它的均值集合和协方差函数集合所确定。

  2. 正态过程的严平稳与宽平稳等价。

  3. 正态过程的不相关与相互独立等价。

  4. 正态随机过程通过线性系统后的输出仍为正态过程。

image.png

[!ERROR] 平稳正态随机过程在这里略掉了喵